Greenpower Car Stabilty
Chipping Sodbury School - 2010-06-30
The Rotary Racer Team
Introduction
One of the things to get right in the design of a Greenpower car is its stabilty on the track. This is especially true for cars that have the aerodynamic and rolling efficiency to go relatively fast, but applies to all cars. This is an attempt to provide some basic information on measuring a cars stability.
This information is based on the experience of past and present Greenpower team members at Chipping Sodbury School and on searching the web and other material for information. It may not be completely correct ...
Cornering
One important factor in a Greenpower cars design is its resistance to rolling over on a bend or when an inexpierienced driver steers sharply. When a car turns there is a centripetal force acting on the car towards the center of curvature that makes the car go round the corner.
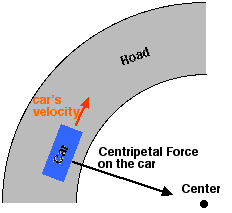
This force is supplied by the sideways friction of the cars tyres on the track. The amount of force needed is dependant on how fast the car is going and how sharp the corner is. This force is calculated by the following equation:
Fc = m v2 / r
Where m is the mass of the vehicle, v is the velocity in meters per second and r is the radius of the turn. An important point here is that the force required is proportional to the square of the speed. Thus the amount of force required goes up quickly when the car gets faster. Note also that the force required is inversly proportional to the radius of the turn. Sharp corners require greater forces. Driving skill is important to driving the car in a racing line around a corner. One aspect of the racing line is to increase the radius of the turn as much as possible to reduce the peak force needed to navigate the corner. Also sudden swerves while going in a straight line are like going around a quick sharp bend, smooth driving is important to reduce the centripetal force involved.
Rolling Stability
So given that there is a sideways force applied to the car, how does the car supply this ?
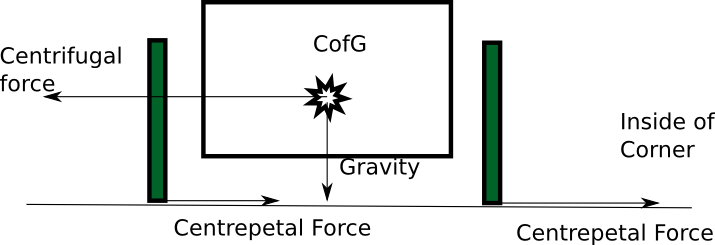
The tyre friction supplies the centrepetal force necessary to push the car off its straight line track. However this force is applied low down at the track. The whole of the mass of the car has to be pushed around. In a Greenpower car the center of mass, commonally called the centre of gravity (CofG), is some way off the ground. Because of this there is a net rotational force trying to roll the car over. The higher the centre of gravity and/or the shorter the distance between the wheels then less centrifugal force needed to roll the car and the more likely the car is to roll on cornering. (Note that centrifugal force is really the effect of the inertia of the mass, it is not really a force, but is useful to help describe the problem).
The tyre friction is proportional to the mass and dependent on the two materials contacting each other and temperature. Normally a coefficient of friction is given between the two materials involved.
Friction = CoF * m
So how can we ensure that a car is stable and can't roll ? Well we can't ensure it unless the CofG was at track level, but we can reduce the likelyhood. One factor is the amount of friction the tyres can exert on the track before sliding. This is limited. As the centrifugal force will always equal the centrepetal force and the centrepetal force is limited by the friction of the tyres, we know the limit of the centrifugal force. So as long as this force is less than that needed to roll the car, the car shouldn't roll when cornering. Unfortunately this is a simplification. It only considers the static case. In real life the car is moving over a rough surface with bumps and various friction levels, the wheels are turning and various other effects occur. However it gives a useful base line figure that is relatively easy to calculate.
Calculating Stability
The first thing to find out is where the centre of gravity of your car is. This can simply be done by a tilt test. With the car fully loaded with driver and batteries and on a flat and level surface, carefully tilt the car on its wheels until it is at its balance point. Now measure the angle between the ground and the cars top or bottom surfaces or bottom of the tyres. We did this using two pieces of wood, a tape measure and a set square. A large protractor can also be used or a digital phograph with a small real or virtual protractor can be used. Here we measured the stability of Rotary Racer RR8e.
 |  |
Using the wood method, the set square is used to make the angle between the ground and the upright 90 degrees and then the three lengths of the triangle are measured.
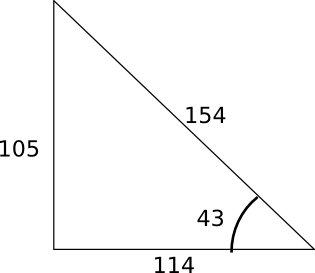
We checked our right angle was about right using pythagorous's theorm.
H2 = O2 + A2 (H - Hypotenuse, O - Opposite, A - Adjacent).
So: sqrt(1052 + 1142) = 154.9, so we were reasonably correct. We then calculated the tilt angle using the inverse TAN function:
angle = atan(O / A)
This gave us the rounded value of 43 degrees. The wheel track of Rotary Racer is 600mm and so we can calculate the height of the center of gravity as follows:
height = (0.5 * 600) / tan(43) = 321mm
 We now measured the sideways force needed to slide the car sideways on tarmac to determine the tyres coefficient of friction on tarmac. We used a simple method to do this some bathroom scales and a pair of feet ! The scales were placed on the cars side (with some stiff protection foam) at about the CofG's height and as close to the front and then rear wheel as possible. The force needed to just get the car to start sliding was noted. As the scales were not placed directly over the wheels we scaled the figures as appropriate after mesuring the distance between the wheels and how far the centre of the scales was from the wheel centres.
We now measured the sideways force needed to slide the car sideways on tarmac to determine the tyres coefficient of friction on tarmac. We used a simple method to do this some bathroom scales and a pair of feet ! The scales were placed on the cars side (with some stiff protection foam) at about the CofG's height and as close to the front and then rear wheel as possible. The force needed to just get the car to start sliding was noted. As the scales were not placed directly over the wheels we scaled the figures as appropriate after mesuring the distance between the wheels and how far the centre of the scales was from the wheel centres.
Now we weighed the car under the front and rear wheels. In the end we had the following figures:
| Driver Weight | 56.2Kg |
|---|---|
| Front Wheels Weight | 57Kg |
| Rear Wheels weight | 88Kg |
| Total Weight | 145Kg |
| Front Slide Force | 63Kg |
| Rear Slide Force | 86Kg |
| Wheel Separation | 1320mm |
| Side force applied | 350mm inside of wheel centres |
| Tilt/Roll Angle | 43 degrees |
| Temperature | 20 degrees C |
We then calculated the corrected front and rear slide forces, based on where the force was applied to the car relative to the wheel positions. This is a simple lever forces problem. There is a pivot point on the far wheel and a friction force stopping movement on the other. The force is applied between the wheels.
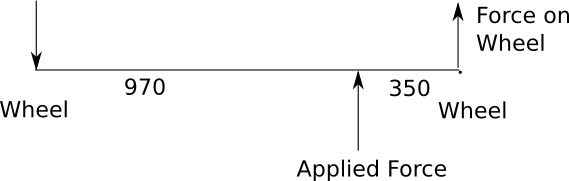
So we can calculate the force on the wheel with:
FslideRear = (FappliedRear * 970 / 1320) = (83 * 970 / 1320) = 64Kg
The total slide force is the sum of the front and rear slide forces:
Fslide = FslideFront + FslideRead = 111Kg
The force needed to roll the car was then calculated:
Froll = tan(43) * 145 = 135Kg
As the force needed to roll the car is greater than the sliding force, the car should slide and perhaps spin, before rolling. However, this is a simplistic static calculation of the rolling stability. The car will be actually moving over a perhaps bumpy track, brakes may be applied, sharp steering movements may be occuring and there may be ridges or kerbs for the wheels to hit. Without going into depth on the issues, we can make sure there is a margin of safety between the slide and rolling forces to reduce the likelyhood of a roll. A simple stability factor can be calculated by calculating the percentage difference between the roll force and slide forces:
Stability = 100 * (Froll - Fslide) / Fslide = 100 * (135 - 111) / 111 = 21%
So we get the following figures:
| Side force Correction factor | (1320 - 350) / 1320 = 0.74 |
|---|---|
| Front Slide Force | 47Kg |
| Rear Slide Force | 64Kg |
| Total Slide Force | 111Kg |
| Force Needed to Roll | 145 * tan(43) = 135Kg |
| Stability | (135 - 111) / 111 = 21% |
| Weight Distribution | 39:61 |
Conclusions
The roll stability of the car is thus dependent on its tilt or roll angle and the amount of friction the particular tyres in use can generate on the surface in use. Lowering the CofG or increasing the wheels track obviously increases the stability, but, if the car hits an obstruction sideways on or has some increased friction in the sideways plane, perhaps by bouncing, the car can still roll no matter how high the stability value. Although Rotary Racer RR8e had a stability factor of about 21%, we have lowered the CofG by 30mm and increased its track by about 20mm. This has increased the tilt angle to about 47 degrees and the stability factor to about 36%. As a secondary safety feature a solidly designed roll-bar should obviously be built in.
From our expierience we would consider that the minimum tilt angle should be 45 degrees but cars should aim to be nearer 50 degrees to give a larger margin of safety.
Note that a tilt angle of about 38 degees will give a stability value of 0%. A car with this tilt angle with the same tyres as RR8 on the same surface would unconditionaly roll with a tight enough turn.
Working out the Stability of a Design
Although it is easy to measure the stability of a car once built, we need to be able to estimate the stability of a cars design before it is built or a lot of time and money (and team morale !) could be wasted. A rough stability value can be calculated using the heights of the centre of mass of the main high weight items in the car. For simplicity these are:
- The driver, possibly 60Kg.
- The car itself possibly 53Kg.
- The batteries 20Kg.
The drivers body is often at an angle to the horizontal in the car. A rough and useful estimate is to measure the height of the shoulder and pelvis mid points. The mid point between these two heights provides a simple estimate of the overal driver CofG. Use the weight of the heaviest expected driver, the driver is probably the highest, heavy weight item in the car and thus could contribute most to rolling. Assuming the car has a cage around the driver, the car bodys CofG will be aproximately the point mid way between the top and bottom of the main chassis ignoring the rollbar.
We have measured the coefficient of friction of bike tyres on tarmac to be in the region of 0.8 (Schwalbe Durano 406) and a standard tarmac surface. The following calculation assumes this, your tyres may be different. The height of the overal centre of gravity can be calculated as:
tyreCof = 0.8 #Tyres coeficient of friction totalWeight = (carWeight + batteryWeight + driverWeight) cofg = (carWeight * carMassHeight + batteryWeight * batteryMassHeight + driverWeight * (driverShoulderHeight + driverPelvisHeight) / 2)) / totalWeight rollAngle = atan((wheelTrack / 2.0) / cofg) stability = 100.0 * ((tan(rollAngle) / tyreCof) - 1.0)
An interactive calculator is at:
Note that this method assumes the masses are at the centre of the wheel track. For asymetric cars you will need to do a bit more maths :)
The choice of what rollAngle/stability factor is reasonable is open to debate. We would suggest that the minimum should be 47 degrees giving a stability factor of about 35%. This gives some margin for different tyre compounds and track surfaces and dynamic issues. With our expierience of the Rotary Racer car, it raced with a roll angle of 43 degrees for a year and a bit including some tight tracks with no problems. However it did roll on a fast, negative camber, with a ridge, tight bend at Castle Combe. Rotary Racer 8 now has a roll angle of 47 degrees.

