Greenpower Car Science and Maths
Chipping Sodbury School
Introduction
There are many aspects to racing a competitive Greenpower car race. These include the cars reliability, the drivers skill, the teams skill the weather plus many others. Although these aspects are important it is also important to get the "science" right.
It is important for engineers to understand the science aspect of their designs in order to understand what is needed and how best to optimise the design for the environment it is designed to work in. The engineer will at least use basic mathmatics in the design process and quite often farily sophisticated mathmatics in calculating parameters and often in simulating the design to test and optimise its function prior to actualy building an example.
This document attempts to describe the science of a Greenpower Electric Car using mathematical equations. Although any mathematical equation describing physical properties in real world situation is always going to be an approximation, the nature of a Greenpower Endurance race and the electrical nature of the Greenpower car allows the basic operation of the car to be relatively and reasonably accurately understood and calculated using a few basic mathematical equations.
To do well in a Greenpower race requires designing and setting the car up to run as fast as possible whilst keeping the power used to a fixed level so that the batteries will last the race. This means focusing on the efficiency of the car, making it go as fast as possible with the minimum amount of power.
This information is based on the experience of past and present Greenpower team members at Chipping Sodbury School and on searching the web and other material for information. It may not be completely correct ...
Forces Acting On the Car
There are three main forces acting on the car:
- The Aerodynamic Drag: This is the force that opposes the movement of the car through the air.
- The Rolling Resistance: This is the force that opposes the movement of the car due to tyre deformation, friction in bearings, friction in drive system etc
- The Drive Force: This is the force generated by the motor to push the car along the road.
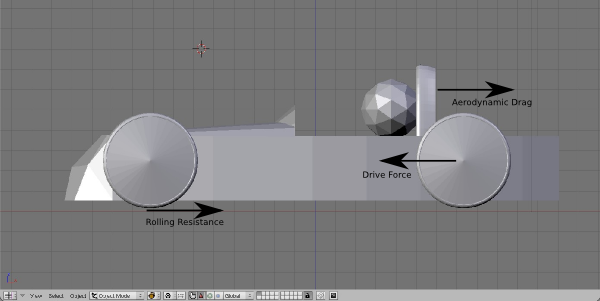
The drive force will accelerate the car increasing its speed until the sum of the Rolling Resistance and the Aerodynamic Drag forces equals the Drive Force being applied. The car will have reached its maximum speed in the conditions that prevail. At this point:
driveForce = rollingResistance + airDrag
The Aerodynamic Drag
The Aerodynamic drag is the drag force caused by the air which the car is moving through. It consists of pressure and viscus drag. A reasonable equation defining this force is given below:
Air Drag, in Newtons:
airDrag = 0.5 * airDensity * airDragCoefficient * carFrontArea * (v * v)
The AirDensity is about 1.17 at sea level at normal air pressure.
The airDragCoefficient is a constant figure for a particular car. It is a measure of how good the aerodynamic shape of the car is. For a good car it is in the order of 0.35. The carFrontArea is the area of the car in square meters as seen from the front. The velocity of the car is given by v in meters per second. To get a lower drag you need a lower frontal area and/or a lower air drag coefficient
Note that the aerodynamic drag is proportional to the square of the velocity. It thus becomes the predominant drag at higher speeds (greater than about 30Km/H). Also note that any wind on the day is effectively added to the cars speed for drag calculations when the car is going into the wind and subtracted when going downwind. As the aerodynamic drag is proportional to the square of velocity you will not save as much power going downwind as you use going into the wind. Hence on a windy day, the overall efficiency of the car will be less.
For more information please see: http://en.wikipedia.org/wiki/Drag_coefficient
Measuring the aerodynamic drag of a car is tricky without a wind tunnel. However, being able to describe the cars performance using maths, allows us to perform some measurements and estimate it. The following two methods require you to first measure the rolling resistance. Two methods are:
- Roll Down Test: Basically find a long length of track (1/2 mile ?). Get the car up to a reasonable speed, say 40 Km/H and let it coast to a halt. Either measure the time it takes to cone to a halt in both directions, or better still data log the speed versis time during the roll down and use curve fitting. Knowing the rolling resistance you can calculate the deacceleration due to the aerodynamic drag force and hence determine this force. http://physics.technion.ac.il/~rutman/car/Roll-down%20test.pdf It is quite tricky to find a safe track long enough to perform this though.
- Calculate From Race Data: A simple way of estimating the Aerodynamic drag or Cd value is to measure the average speed of your car while racing and then knowing the rolling resistances and either the average current being used or the gearing and wheel diameter you can estimate the Cd. The motor and gearing equations will provide you with the drive force at a particular current or speed. This allows you to calculate the aerodynamic drag force. You can use the maths on this page to work this out or plug values into the car speed calculator at: http://portal.beam.ltd.uk/greensim/CarMaths.py until you match your cars performance. In this case put in all the known values and then modify "Air Drag Coefficient" until the simulation matches the speed of your car.
The Rolling Resistance
This is predominantly produced by the deformation of the tyres as well as bearing and drive system (chains, gears etc) friction. Its magnitude is approximately proportional to the cars weight (mainly tyre deformation). A reasonable equation defining this force is given below:
Rolling Resistance, in Newtons:
rollingResistance = rollingCoefficient * mass * 9.8
The Mass is the overall weight of the car in Kg including the car, batteries and driver.
The rollingCoefficient is a constant figure for a particular car. This needs to be measured. For a car with low rolling resistance tyres at a high pressure and with a simple chain drive it is in the order of 0.005.
Going up a hills also increases the force needed to go up the hill. However this force is directly proportional to the cars mass and so the energy we use pushing the car up the hill will be recovered when we go down the hill as we race on circular tracks. Apart from the efficiency changes and extra aerodynamic drag caused when going down hill (not canceled completely out when going slower uphill), the small hills on racing circuits have little overall effect on a Greenpower cars race.
For more information please see: http://en.wikipedia.org/wiki/Rolling_resistance
It is possible to measure the rolling resistance using a spring balance that measures up to about 20N. To do this:
- Find a fairly level piece of tarmac.
- With the car fully loaded pull the car with the spring balance at a steady speed and note the average force in Newtons. It is tricky to keep a steady speed. Adding an additional spring or elastic band can smooth the readings a bit. Perhaps pulling the car with a slow RC/car would give a more consistent reading than a human pulling it. F1.
- Perform the above measurement in the opposite direction and average out the values. F2. F = (F1 + F2) / 2.
- The rolling coefficient, Cr would be: Cr = F / (mass * 9.8)
The Drive Force
This is the drive force produced my the motor at the wheel of the car.
The amount of force produced is a combination of the electrical voltage, the electrical current passing through the motor, the speed of the motor,the gearing of the motor to the wheel and the diameter of the driving wheel. As an electrical motor has a specific Torque curve verses the electrical current and rotational speed, this needs to be taken into account.
The following equations reasonably accurately model the Greenpower Fracmo motor:
motorTorque = (voltage / 24.0) * (13.5 - (motorRpm * 13.5 / 2060.0))
The Greenpower Fracmo Electric Motors Torque curves are given here.
The DriveForce produced at the rear wheel by the motors Torque is dependent on the gearing and size of rear wheel. The equation for this is:
speed (Km/H) = 3.6 * (3.14 * wheelDiameter) * motorRpm / (60 * gearRatio)
The Motor Temperature
As the current through the motor is increased its efficiency drops. This is due to the heat generated by the windings resistance. The Fracmo motor has a winding resistance of about 0.18 Ohms at 20 degrees C. The heat generated at 17Amps is thus about (17 * 17) * 0.18 = 52 Watts (from P = I2 x R). Thus at 17Amps the motor is using: (24 * 17) = 408Watts of which: 52Watts is lost in heat and (408 - 52) = 356Watts is available to move the car. The motors efficiency at 17Amps is thus: (100 * 356 /408) = 87%. Note that this is ignoring mechanical losses in the motor so the efficiency will be a bit less than this.
Note also that the winding resistance increases with temperature and thus the motors efficiency goes down further with armature temperature. The temperature coefficient of copper is 0.0039. If the windings heat up by 30 degrees C the resistance will increase by: 30 * 0.0039 * 0.18 = 0.021 Ohms. This will result in a decreased efficiency of: 100 * 0.021 / 0.18 = 12%.
Note also that this is based on the temperature of the motors armature. The motors armature will be at a higher temperature to the motors case as there is a degree of "thermal resistance" between the armature and the motors case.
Note that the heat generated is: I2 x R. Thus the heat generated is the square of the current drawn. In fact due to the fact that winding resistance increases with temperature, the heat generated is more that a square law on current. For a cool, efficient (and non burnt out :) ) motor it is imperative that the average current is kept low (less than 17 Amps). The selection of a suitable gear ratio for the car in question in the conditions prevalent on the day is thus essential. An interactive motor temperature calculator is at:
http://portal.beam.ltd.uk/greensim/CarMaths.py
As a little experiment it is possible to measure the temperature of the motors armature by making use of the fact that the resistance of copper changes with temperature. One method would be:
- With the motor cool pass about 1Amp through the stalled motor from a bench power supply that has a current limiting function. Measure the current and voltage accurately with two multimeters. Note the temperature, current and voltage. t1, i1, v1. Resistance r1 = v1/i1.
- Perform the same measurements soon after the motor is at running temperature (outside case 40C ?). t2,i2,v2. Resistance r2 = v2/i2.
- The armatures temperature will be approx: ta = t1 + (r2 - r1) / (0.0039 * r1)).
- Note that due to the comutator you may have to turn the motor for the minimum reading on each measurement.
Batteries
In a Greenpower race we have limited energy available from the 4 batteries. So although the current into the motor will vary during the race, we have to make sure that the average current is not greater than that which the batteries can put out for the entire race without going flat. With a Greenpower 4 hour race using, good condition, standard Greenpower MRT35 batteries at reasonable temperature (20 degrees C)) this is about 17 Amps. Thus at 24 Volts we have an average power of 24 Volts * 17 Amps = 408 Watts of input power available.
This limits the drive force that we can use, on average, throughout the race and thus sets the maximum average speed we can attain.
Battery Discharge
The physics and chemestry on how a lead acid battery works is quite complicated. However the discharge characteristics can be approximately modeled using Peukert's_law. The core algorithm is:

T = H / (I * H / C)^k
- T - Discharge time in hours
- H - Battery discharge rate time (20 hour rate)
- I - Discharge current
- C - Battery capacity at stated discharge rate (75 amp/hour)
- k - battery constant between 1.1 and 1.3 depending on battery type and condition.
For use in calculation a discharge value over a time period:
c = I * T * pow(I / Ir, k - 1)
- c - Amount of charge to take away from total charge
- I - Current
- T - Time period in hours
- Ir - Current for battery amp/hour rating (For 75Amp/hour at 20hour rate = 3.75)
- k - battery constant between 1.1 and 1.3 depending on battery type and condition.
This is taken from info at: http://en.wikipedia.org/wiki/Peukert's_law
There is more info at: http://www.thermoanalytics.com/support/publications/batterymodelsdoc.html
More info at: http://mocha-java.uccs.edu/dossier/RESEARCH/2002evs19a-.pdf
This looks like it is reasonably accurate for the batteries we use based on the battery discharge tests performed. A k value of about 1.2 is about right for the MRT35 batteries.
The Battery voltage is calculated using:
Et = Eo - Ri*I + Ki*log(Ct/C)
Where- Et = battery terminal voltage [volts]
- Eo = open circuit voltage of a battery cell when fully charged [volts]
- Ri = internal (ohmic) resistance of the battery [ohms]
- Ki = polarization resistance [ohms]
- I = instantaneous current [amps]
- C = current charge level in amp/hours
- Ct = total battery charge in amp/hours
Drive Forces Versus Speed
Given the above equations, we can plot the forces in operation on the car versus speed. Plotting the equations results can help us understand what is happening better. The following graphs are for a Greenpower car having a rollingCoefficient of 0.01 and an Aerodynamic coefficient of 0.60 and a frontal area of 0.5 meters square.
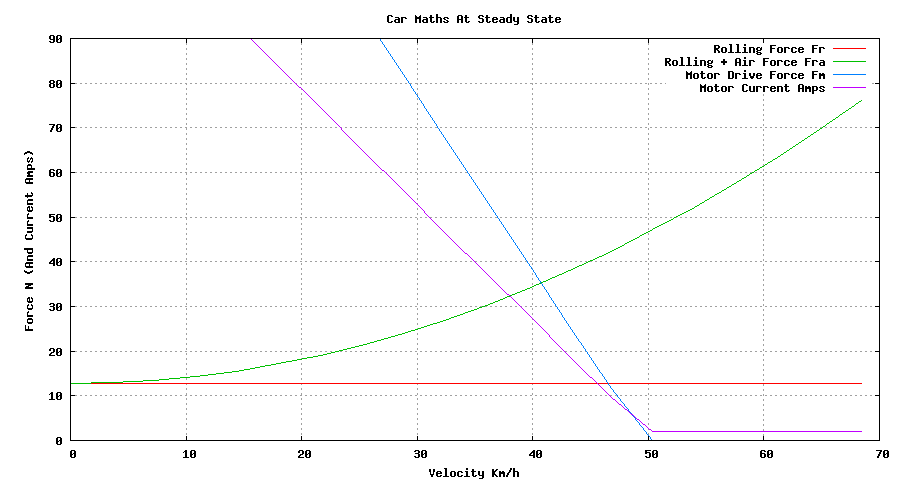
Note that the motors drive force decreases linearly with increasing speed. The Motor equations describe this process. The Rolling Resistance force is a constant with respect to speed. The Aerodynamic Drag however is proportional to the square of the speed. The point where the Green and blue line crosses will be the point of equilibrium where the forces balance. This will be at the maximum speed of the car.
There is an interactive car drive force calculator in the following link that allows you to try different gear ratio's etc.
Conclusions
After looking into the science and maths how do we get a better performing car ?
-
Better Aerodynamics: The main force holding the car back will be the Aerodynamic drag. The cars aerodynamic profile needs to be addressed.
-
Lower rolling resistance: high pressure, low rolling resistance tyres are best with an efficient drive system (chains or gears). The cars weight should be kept as low as possible.
-
Gear setting: The gearing of the motor needs to be set so that drive force balances with the aerodynamic and rolling resistance forces when the motor is drawing about 17 Amps. Either a well set fixed gear, changeable gears or fixed gear with motor speed controller can be used.
-
Motor cooling: The motors efficiency drops by 19% with a 50 degree C increase in temperature. Also this is a positive feedback system. Ie if the temperature increases, the motor produces less power and the car slows down. When the car slows down the motor will take more current which heats it up more and so on.
More Information
There is a Car Maths Calculator at: http://portal.beam.ltd.uk/greensim/CarMaths.py
There is a Greenpower Car Simulator that uses the mathematical equations given here to simulate a Greenpower car going around a track and display the graphs of various parameters. It is located at: http://portal.beam.ltd.uk/greensim.
There is info on setting the gear ratio at: Setting the Gear Ratio
There are data sets from the Rotary Racer Greenpower car measured by the Car Computer at various races at: http://portal.beam.ltd.uk/greenpower/files/RotaryRacer/performance
There is a very useful document on building Greenpower cars on Greenpowers site. This is: Greenpower A-Z Guide

